Latency vs Probability of Collisions

This post is based on a presentation I recently delivered – the first time at WLPC EU 2023 in Prague, CZ and the second at #MFD10 Ignite in San Jose, CA.

According to statisticians, variations from the average are more relevant than the average itself. This complication often plays out at theme parks or concession stands. Have you ever been at an amusement park, waiting in line for hours, thinking, “If they just had one or two more roller coasters, all the lines would be shorter”? While it may seem that adding attractions would lead to quicker queues, it’s not the case.

Why is this? According to statisticians, and using the example of Disney World, the varying pattern of when guests arrive at the ride, and not the average number of guests arriving, makes the lines so mind-numbingly long. Since lines form when demand exceeds capacity, it seems logical that if Disney World accurately predicted demand, they could build capacity to accommodate it. Unfortunately, it’s not so simple. 

Statisticians are positive that even if Disney could accurately predict the number of park visitors hopping on the Rise of the Resistance on a peak day, a line would still form because guests queue up at irregular intervals throughout the day, and the ride’s capacity remains fixed. Planning for capacity can deal with average demand rises but not fluctuating demand. 

Disney has dealt with this issue using a ride ticketing feature called FastPass, which entitles guests to return to a ride at a designated time and jump into an express lane. FastPass works because it reduces the variability of guests arriving at any time. While it doesn’t change the ridegoers’ actual waiting times, it does give them the freedom to enjoy other activities in the meantime, thereby boosting customer satisfaction. 

The vast size of the universe is truly mind-boggling and can be quite challenging to comprehend. It’s difficult to express just how big it is. The universe contains billions of galaxies, each with billions of stars. To give you an idea, think of our Milky Way galaxy: It’s estimated to be about 100,000 light-years in diameter, which means that if you could travel at the speed of light, approximately 300,000,000 m/s, it would take you 100,000 years to go from one end of our galaxy to the other. The distances between celestial objects, even within our own galaxy, are incredibly vast. For example, the closest star to our Sun, Proxima Centauri, is about 4.24 light-years away. That’s trillions of kilometres. The distance to our nearest neighbouring galaxy, the Andromeda Galaxy, is about 2.537 million light-years away. We have pentameters of empty space or nothingness between all these celestial bodies.

Using the frame reference of space and distance between celestial bodies, let’s apply a model to some spectrum captures and figuratively represent our universe and the space between transmissions. Einsteinpublicized the Space-Time domain, which we will reframe as the … Space-Airtime domain.

Scrutinizing spectrum traces with the perspective of wireless activity across the space-airtime domain of our universe unveils there is a lot of space between transmissions. There are, of course, other wireless transmissions from non-Wi-Fi devices like BLE, Zigbee, microwaves, LED lights, audio, and video radiators. Transmission from these non-Wi-Fi devices is similar to the interference and chaos caused by meteors, asteroids, and comets hurling across space-time.

Just as the universe is boundless, so is time. What if we imagined the time frames transmitted similar to the space consumed by celestial objects? Let’s break up that space into units of time. What would be the smallest unit of time?

The term “atom” comes from the Greek word “atomos,” which means “indivisible.” Historically, it was once thought that atoms were the smallest, indivisible units of matter. However, with advances in science, we now know that atoms are composed of smaller particles.

So we’re not looking to define the absolute smallest unit of time, just something small enough to represent the atom.

Could the smallest unit of Wi-Fi time be Transmit Opportunities (TxOP)? No, there is too much variability between TxOps. Time Units? Even the name sounds like a good candidate for the smallest unit.  There are standard intervals based on time units. For example, 100 TU represents a standard beacon interval.

What about slot time? Slot times are short and static time intervals, but there are some different values of slot time, based on the band/technology.  An individual slot time does not seem significant at the scale of Wi-Fi time, but for humans, a 20s period represents 2.2 million timeslots.  How many frames could be transmitted within such a window? Perhaps more worrisome is how many time slots would be empty or idle when transmitting using Wi-Fi. Empty time slots are moments that could have been used to transmit data. Just as there are vast voids between our celestial bodies, there is a vast void between Wi-Fi frames. In short, Wi-Fi as a protocol is wildly inefficient.

To be better custodians of finite Wi-Fi bands in the wireless spectrum and make better use of space-airtime, there needs to be a mechanism to fill available time slots while at the same time avoiding collisions. For every collision, the same bits must be resent and transmitted for a second time, consuming additional time slots.

Wi-Fi, at least for the moment, is a half-duplex medium, although Wi-Fi 8 has the potential to make it full-duplex in the future. Radios infer collisions post hoc… but even then, it might have just been interference causing the signal corruption, not necessarily a collision.

This brings us to one of the defining challenges in Wi-Fi – Greg Ennis (author of Beyond Everywhere – How Wi-Fi Became the World’s Most Beloved Technology) describes the debates between distributed and centralized protocols pre-802.11 standard and how a compromise of including both in the standard won the vote, ultimately leading to the amendment of the original IEEE802.11 standard. The way compromises and inefficiencies in the IEEE occur is perhaps a parallel to why democracy is inefficient but imaginably better than having the wrong committee chair at the helm.

Care must be taken in Wi-Fi networks to avoid transmitting simultaneously as another transmitter. When a frame is queued up and ready to transmit, it’s fairly easy to check if another transmitter is already active. The challenge of detecting a collision exists when two transmitters unknowingly transmit simultaneously. Even here, collisions are not directly detected; rather, they are inferred when the transmitting radio does not receive an Acknowledgment (ACK) frame returned by the receiving radio, confirming its successful reception of the frame. Collisions can significantly impact network performance, and there is a penalty associated with them.

Collision avoidance is described as the Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) mechanism. Ethernet, on the other hand, uses collision detection (CD), which has a dedicated transmit and receive path allowing full-duplex operation. Ethernet can listen while transmitting and detect collisions in real-time – triggering a jamming and backoff process when necessary. Wi-Fi cannot directly detect collisions and is designed to reduce the likelihood of them occurring in the first place. Here’s an overview of what happens in CSMA/CA:

• Interframe Space (IFS):
  • A scheduled gap in time (number of slot times) following the end of a frame transmission. The length of the gap is fixed, but the actual value varies depending on the frame that was most recently transmitted or, if QoS is enabled, the configured value for the access category.  There are many types of IFS – non-QoS uses DIFS, QoS uses AIFS, and SIFS are used before transmitting control frames.
• Randomized Backoff:
  • Before transmitting a frame, the sender enters a backoff period. This backoff period is chosen randomly from a range defined by the Contention Window (CW). The CW starts at a minimum value and may double in size for each subsequent collision (a process known as exponential backoff). The larger the CW, the longer the backoff period.
• Clear Channel Assessment:
  • Before transmitting a frame, the sender completes two assessments to measure if the wireless medium is busy. These two checks are:
  • Physical Carrier Assessment:
    • The physical assessment is made up of two detection mechanisms:
    • Energy Detect (ED):
      • Energy detection listens for raw RF energy measured above a threshold of -62dBm (per IEEE 802.11).
    • Physical Detect (PD):
      • Physical detection involves listening to other Wi-Fi frames. At this stage, only the physical (PHY) header is demodulated – not the full frame. PHY headers are sent at 6Mbps in 5/6GHz and at 1 or 2 Mbps on 2.4GHz – ALWAYS. It does not matter what data rates you disable in your configuration; the PHY layer modulation is not impacted. A value for the time the transmitter will occupy the medium is coded in the PHY header, informing all receivers how long to defer.
  • Virtual Carrier Assessment:
    • The final check demodulates any Wi-Fi frames received at layer two, reading the network allocation vector (NAV) value. The NAV timer indicates how long the active transmitter has reserved the medium or how long the receiver must defer before entering the CW.
• Collision Detection:
  • When a device (e.g., a station or Access Point, although the IEEE describes both as a client device and access point using the term station) sends a data frame, it listens for an ACK frame. If the sender does not receive an ACK within a predefined time frame, it assumes a collision occurred.
• New Transmission Attempt:
  • The sender makes a new transmission attempt once the backoff period expires and the wireless medium has not tripped the busy threshold. The sender will again listen for an ACK frame. If it receives the ACK, the frame is considered to have been transmitted successfully – a successful TxOP.
• Penalty for Collisions:
  • Collisions result in a performance penalty for the network. Here’s why:
  • Collisions consume valuable airtime, causing delays in data transmission.
  • The exponential backoff mechanism ensures that devices with multiple collisions wait longer, reducing their chances of transmitting.
  • As the CW doubles, the contention window becomes larger, and the chance of a collision is reduced. However, larger contention windows also mean that devices may need to wait longer before attempting to transmit again.
• Data Rate and MCS Selection:
  • In most Wi-Fi networks, the data rate or Modulation and Coding Scheme (MCS) is adaptive. It can vary based on signal strength, interference, and noise. However, a specific collision doesn’t inherently dictate a change in data rate or MCS.
• Retransmission Limit:
  • Many Wi-Fi devices have a retransmission limit for data frames. After reaching this limit without a successful transmission (often due to collisions), the device may drop the frame to prevent continuous retransmission attempts.
• Channel Congestion:
  • Collisions, especially in high-traffic or congested environments, can significantly impact channel efficiency. Collisions lead to retransmissions and increased contention for the channel, which results in more delays.

Reducing collisions is a key goal in Wi-Fi protocol design, as they can degrade network performance. Strategies like efficient network design, QoS mechanisms, appropriate use of RTS/CTS frames, and minimizing hidden node issues can help reduce the probability of collisions and their associated penalties.

Wi-Fi is an extremely polite protocol. Sometimes, it behaves like two Canadians arguing about who should walk through the door first – each insisting the other go first. In this sense, Wi-Fi is a Canadian protocol, with each radio deferring to another, waiting for the other to go first – it’s a dance off bro!

Now that we have discussed the background theory and mechanisms of CSMA/CA, let’s look at an example with VoIP over Wi-Fi (VoFi) traffic.

What happens when you have multiple devices on a voice call simultaneously connected to the same radio?How many time slots will each client require to sustain a voice call? Complicate this further by interleaving background updates with lower-priority applications (i.e. email, app notifications, etc…). Is it possible to avoid collisions? Are there enough time slots left over between the frames transmitted by other radios, or will the frames collide and smash into each other like the Theia. (Theia is a theoretical planet estimated to be similar in size to Mars, which collided with the Earth. All the debris from this collision was collected in an orbit to form the moon.)  

This is just one example of why collisions are bad – however, the Wi-Fi of the universe is designed to continue if they happen. Ignoring the hidden node problem, the only time two more transmitters should collide is if they all have data to transmit, know other Wi-Fi radios are transmitting, and all transmitters count down to zero at the same time.

VoIP applications work by listening to audio and packetizing that data in 20ms chunks. Those packets then require access to the wireless medium for transmission. Waiting longer than 20ms to packetize data creates noticeable gaps in the audio stream and distracts listener(s) on the other end of the line. An additional complexity with VoIP is that it’s not super receptive to delays or variations in the timing between frames.

During the CW, radios queuing voice payloads roll a 16-sided die (0-15) – when QoS is disabled. A bell-shaped curve is also called a “normal distribution.” The middle of the bell curve represents the number most likely rolled, and the least likely rolled numbers are spread to the left and right along the curve. Making this curve more comfortable for Wi-Fi practitioners, the bell curve is overlaid on top of a DSSS spectrum capture.

A brief tangent about statistics and marketing. Average values are tools of stereotypical sales and marketing. The average value can mean many things, and any statements about an “average” value should be treated with a healthy dose of skepticism. The average could represent the mathematical average, mean, median, or mode. 

The mathematical average is the sum of all values in a set divided by the number of items. The mean is used for normal distributions.  

• Mean is not a robust tool since outliers largely influence it (think average Geography graduate salaries from the University of North Carolina – the same college Michael Jordan graduated from).
• Median is generally used for skewed distributions. The median is better suited for skewed distributions to derive at a central tendency, since it is much more robust and sensible. 
• Mode defines the number that occurs most often in the data set.

A bell curve is a statistical distribution that is often used to represent the probability distribution of a continuous random variable. However, a 16-sided die (or die with any finite number of sides) does not follow a normal distribution because it’s a discrete random variable. Instead, you would typically use a uniform distribution to represent the probabilities of rolling each number on the die. A uniform distribution implies that each outcome (in this case, each of the 16 sides of the die) has an equal probability of occurring. Again, to make this more relatable for Wi-Fi practitioners, a uniform distribution is overlaid on top of an OFDM signal, as shown below:

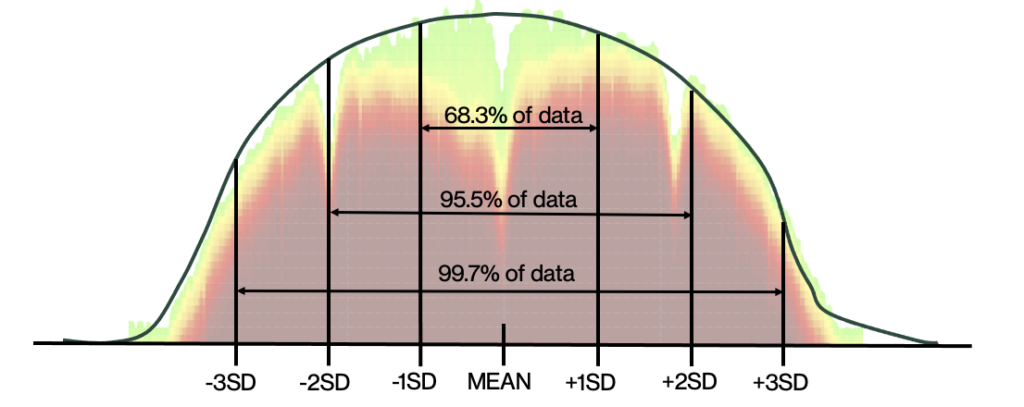
Now, to determine the probability of rolling a specific number (say, 7) on the 16-sided die, you can use the fact that each outcome is equally likely in a uniform distribution. The probability of rolling any specific number is 1 divided by the total number of possible outcomes, which is 16. So, the probability of rolling a 7 is 1/16.

Remember, properties of the normal distribution, such as the bell curve, mean, median, and standard deviation, do not apply to discrete uniform distributions like those of dice. Instead, uniform distributions have equal probabilities for each outcome.

Sprinkle in a little QoS

What has been described so far is a time before QoS. If we flash forward to the era during which QoS appeared in the Space-Airtime domain, we see changes to the IFS space. What was previously a static IFS becomes a variable length AIFS based on the traffic classification as mixed traffic types are scheduled to fill slot times. AIFS aims to reduce the delay and increase the probability of transmitting higher-priority traffic while not starving out lower-priority traffic. The high-priority – voice queue – is not a strict priority queue that serves the high-priority queue until it is drained at the cost of delaying lower-priority packets.

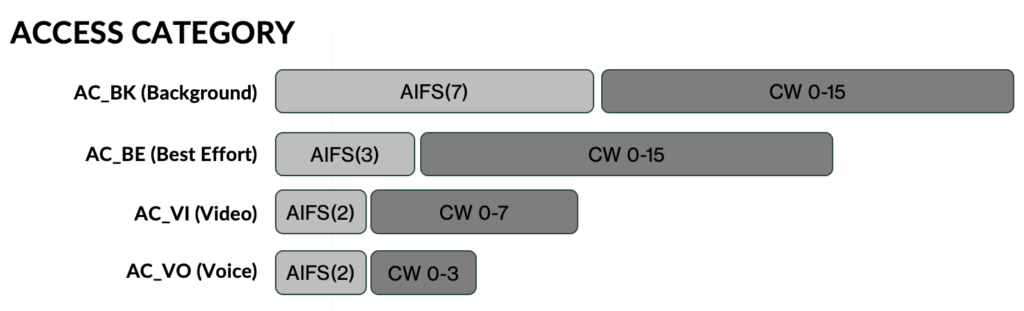
Within the 802.11 standard, there are four queues, as listed below, with default AIFS numbers listed:

• Background (AIFSN 7 / CWmin/max = 15/1023 )
• Best Effort (AIFSN 3 / CWmin/max = 15/1023 )
• Video (AIFSN 2 / CWmin/max = 7/15 )
• Voice (AIFSN 2 / CWmin/max = 3/7 )

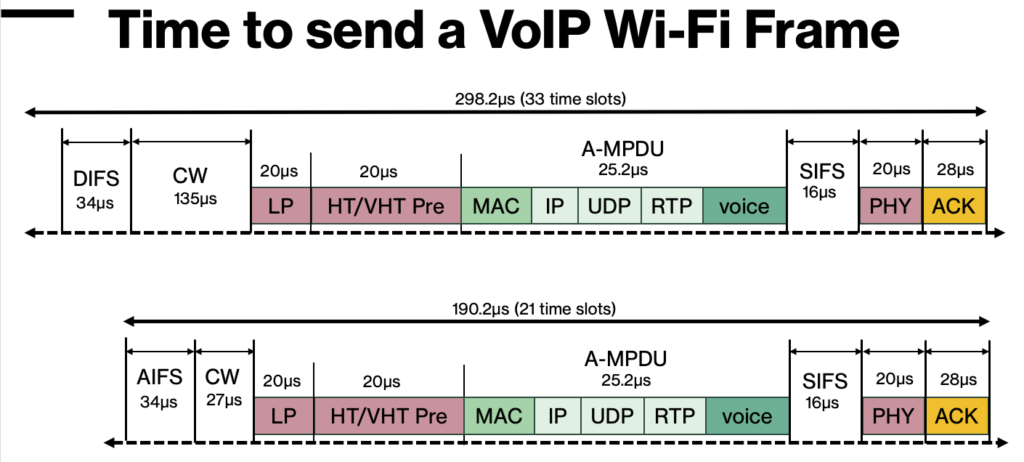
The image below shows a rough comparison of the Space-Airtime (slot times) consumed when sending each of these two VoIP (G.711) frames. The frame on top is sent without using QoS, while the bottom frame has QoS enabled. Changing nothing else about the frame, the impact of reducing the IFS and using a smaller dice (default VO uses 0-3) results in a 30% reduction of airtime or roughly the equivalent of 33 vs 21 slot times.

Markov Chain

Focusing on efficiency and validating efficacy, is there a model that could calculate the probability of radios being in a state of transmission or idle? Is it possible to model the likelihood of more than one radio being simultaneously in a state of transmission?

The Markov chain model is named after the mathematician Andrey Markov. It is a stochastic model describing a sequence of possible events in which the likelihood of each event depends on the state reached in the previous event. In probability theory, a stochastic or random process is a mathematical model defined by a sequence of variables, some of which are random, indexed over a sequence of time. Stochastic models are often used to model the growth of bacteria, electric fields fluctuating due to thermal noise, signal processing, or weather prediction.

To wrap your head around the Markov model, imagine you have a magical blue telephone booth. Call it a TARDIS, and it can take you on an adventure, but where it takes you next depends only on where you are right now. This is a Markov chain – a way to understand and describe things that change over time, like the weather or a game. 

For a practical example, imagine that a system starts in a certain “state,” the starting point – which we can call sunny. There is a list of other states to transition from “Sunny.” Each of these states has a chance of happening. For example, from “Sunny,” the state might transition to “Cloudy” with a 15% chance, or “Rainy” with a 5% chance, or remain “Sunny” with an 80% chance.

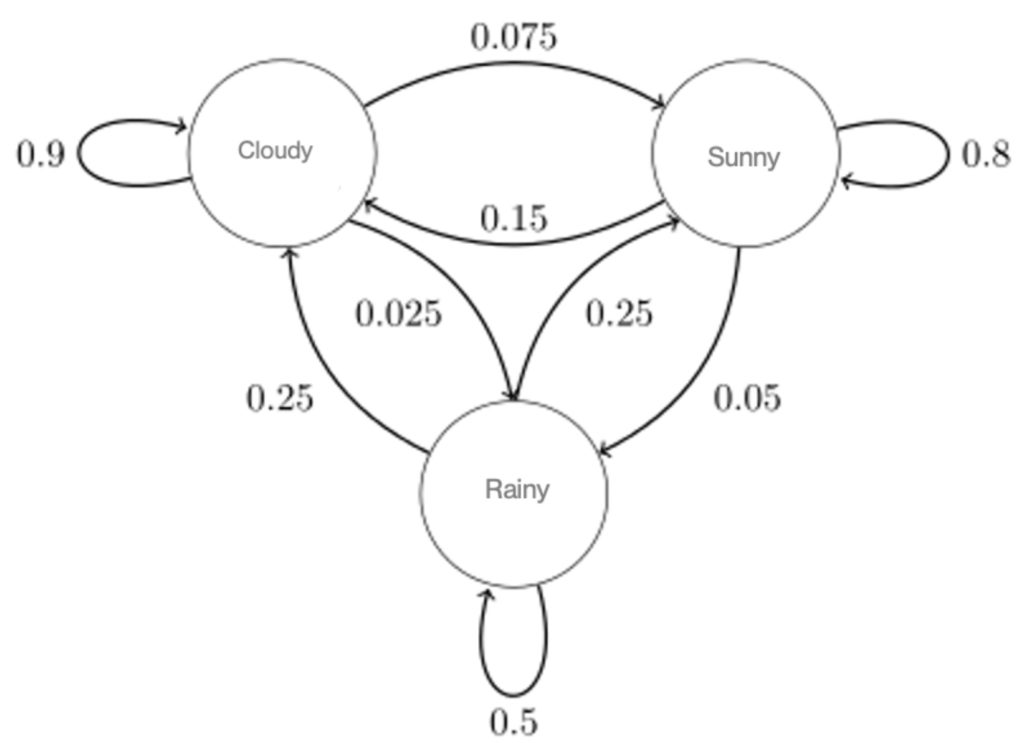
This is a relatively simple model for showcasing the Marko model as applied to simple weather state transitions. Within the context of Wi-Fi, the state of any given radio could be reduced to two states:

1. Idle – not transmitting and completely idle or with a frame queued up to transmit and contending for access to the wireless medium.
2. Transmitting – transmitting of occupying airtime while bits are hurled across the air.

An example of just some of the components that could contribute to the probability of switching to a transmitting state could include:

• probability of a frame queued up in the radio, waiting to transmit
• layer 1 channel utilization
• layer 2 channel utilization
• number of radios on the same channel (includes APs and all clients)
• number of retry attempt(s)
• probability of OBSS created by neighbouring WLAN radios in a transmit state

Some researchers have modelled the efficiency of Wi-Fi using such parameters. Of course, the model becomes exponentially more complicated as more factors are introduced, which can contribute to the likelihood of entering the transmitting state. Two examples of such research come from Giuseppe Bianchi, who wrote a paper called Performance Analysis of the IEEE 802.11 distributed coordination function (DCF) [non-QoS]. Later, he co-authored a paper with Illenia Tinnirello – Rethinking the IEEE 802.11e EDCA Performance Modeling Methodology [with QoS].

What defines efficiency?

These complex models make it challenging to model and optimize schedulers for OFDMA. This also makes it challenging to measure the efficiency of Wi-Fi. Depending on the mix of traffic and modulation, it is possible to measure higher throughput when using OFDM vs OFDMA, but does this mean OFDM is more efficient? When reducing the number of TxOps, we reduce the potential for possible collisions, thereby increasing the efficiency of Wi-Fi. While OFDMA may not always achieve greater throughput, a better measure of efficiency is a measure of latency & jitter reduction in critical applications. 

Payloads sent to or from multiple client devices bundled together using joined resource units (RU) result in fewer TxOps – resulting in lower latency and jitter between payload transmissions.

Slàinte!

Resources

The Wi-Fi Airtime Calculator by Gjermund Raaen

The WiFi AirTime Calculator

Beyond Everywhere: How Wi-Fi Became the World’s Most Beloved Technology by Greg Ennis

Performance analysis of the IEEE 802.11 distributed coordination function by Giuseppe Bianchi

https://ieeexplore.ieee.org/document/840210

Rethinking the IEEE 802.11e EDCA Performance Modeling Methodology by Ilenia Tinnirello & G. Bianchi

https://ieeexplore.ieee.org/document/5288559

---

Also check out these great videos from Andrew McHale detailing Voice over Wi-Fi.

Effects of 802.11k/r/v | Andrew McHale | WLPC Prague 2019

10 Wireshark Tips in 10 Minutes | Andrew McHale | WLPC Prague 2022

Why Are Clients Sticky | Andrew McHale | WLPC Prague 2018

Voice Traffic Protocol Analysis | Andrew McHale | WLPC Prague 2018